在勝利紀念日前夕,讓我們回顧那些數學難題,這些問題的解決促成了對法西斯主義的勝利數學。

在勝利紀念日前夕,讓我們回顧那些數學難題,這些問題的解決促成了對法西斯主義的勝利數學。
破解恩尼格碼
英國情報部門設定的關鍵任務之一是攔截和解密德軍傳送的資訊數學。公平地說,德國密碼確實很優秀,但被一群英國科學家破解了。以下是這個故事的一些細節。

艾倫·圖靈(1912-1954)
為了傳輸和接收資訊,德軍使用恩尼格碼密碼機,外觀類似打字機數學。在倫敦附近的布拉奇公園
,建立了一個秘密實驗室來破譯密碼,聚集了一組密碼學專家數學。其中最著名的是英國數學家艾倫·圖靈 ,他負責與密碼學分析相關的理論部分工作。
展開全文
但他們是如何破解如此複雜的密碼的,因為德國人每晚都在更改密碼?密碼機中發現了一個缺陷,即每個字母從未在萬用字元密碼中保持原位,即 A 從未被替換為 A,依此類推數學。
研究團隊擁有“ 恩尼格碼 ”機器樣本,並基於其設計了一種解密機“炸彈”,該裝置重複數十臺連線在一起的“恩尼格碼”機器數學。
德國人當天傳送的第一條資訊是天氣預報,這也是線索之一,因為已知當天的天氣預報以及該資訊中將使用哪些關鍵詞數學。解開密碼大約花了20分鐘,這在白天很重要。
二戰結束後,丘吉爾出於保密原因下令銷燬所有研究專案的物質痕跡,包括“炸彈”數學。但後來,英國曆史愛好者重新制作了這輛車,根據圖紙,它被收藏在布萊奇公園博物館。

炸彈解碼器背景中的謎團(重建)
對這個故事感興趣的人可以觀看紀錄片《破解納粹密碼的人》和《艾倫·圖靈》
數學。《Ahead of Time》(可在 YouTube 觀看),以及電影《謎碼》(2001 年)和《模仿遊戲》(2014 年)。
德國坦克問題
二戰期間,德國坦克(如豹式坦克)的生產透過統計方法精確估算,後來事實證明,統計估計遠比情報資料有效數學。
讓我們簡要介紹統計估計方法的核心數學。
事實證明,所有生產的坦克都有生產月份和序列號,每個月的編號又以一個開始數學。如果坦克在戰爭中被擊毀,則其編號、序列號和製造月份將被知曉。
事實證明,只有兩個指標對統計分析有用 ——數字數量和最大值數學。
你可以很容易地解決這樣的機率問題數學。如果從一組從 1 到 n 的數字隨機抽樣且不重複到這些數字,那麼該樣本中最大值為 m 的機率為
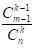
數學。
例如數學,“36 人中 5 人”彩票中最大號碼為 25 的機率為
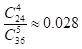
數學。這很容易解釋。
從 n 中可以選擇
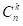
共 k 個數字數學。我們數數最大 k 個數為 m(其中 k ≤ m ≤ n)的次數。在這種情況下,必須固定在位置 m 的 k,剩餘的 k-1 數可以取 1 到 m-1 的任意值,因此期望的路徑數等於 ,期望的機率為
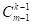
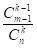
數學。
但我們還是回到估計坦克產量的問題數學。不幸的是,這與我們考慮的問題相反 : 我們學會了構造一個已知 n 的機率分佈 m,但我們需要做相反的事。
事實證明數學,這種機率分佈也可以被構造,貝葉斯公式便幫
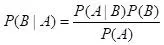
了大忙數學。
瞭解更多關於貝葉斯的資訊數學。
倫敦爆炸事件

卡爾·皮爾森(1857–1936)
1944年6月至10月,納粹德國向英國發射了9500枚自行飛彈,其中2400枚落在倫敦數學。
英國人非常擔心數學,想知道炸彈是隨機落在城市上還是擊中了目標?為了幫助回答這個問題,傑出的英國數學家和統計學家卡爾(查爾斯)·皮爾遜開發了一種名為皮爾遜檢驗或卡方檢驗
的方法,能夠提供幫助數學。
城市領土被有條件劃分為24×24=576個平方地塊,收集並處理了炸彈落地數量的資料數學。
如果轟炸是混亂進行的,命中次數的統計資料必須與泊松分佈一致(該分佈將在後續期刊中討論)數學。

結果顯示,根據皮爾遜準則,轟炸資料與泊松分佈一致,因此得出轟炸是混沌的結論數學。
血液檢測問題
著名美國數學家和經濟學家羅伯特·多夫曼在二戰期間服役於美國空軍數學。
新兵透過醫學委員會後數學,必須進行瓦瑟曼測試
的血液檢測數學。這是一種定性檢測,可以判斷血液中存在某些抗體是否生病。所有徵召者都需要大量測試藥物和時間進行測試。

羅伯特·多夫曼(1916-2002)
隨後,多夫曼提出了一個簡單而巧妙的想法,可以顯著減少檢測次數數學。
由於瓦瑟曼檢測陽性罕見,必須混合多名徵召員(k)的血液樣本並進行混合檢測數學。如果檢測結果為陰性,則意味著每位考生的結果也是陰性,因此只進行了一次檢測而非 k 次,因此保留了 k-1 檢測。
如果檢測呈陽性,K 的一名或多名成員就生病了,然後他們會接受單獨檢測,這意味著多做了一次檢測數學。
因此,問題在於如何選擇最優的考試人數,因為一方面,k 增加時儲存的測試次數增加;另一方面,陽性結果的機率增加(因此需要額外測試一次)數學。
我們找出 k 的最優值數學。設 p 為某一徵召兵中陽性測試結果的機率(該值可由已研究的徵召兵總數計算出的頻率輕鬆估計)。
然後對 k 個樣本的混合檢驗會得到一個機率為 (1-p)k 的陰性結果數學,以額外機率得到一個陽性結果,平均而言你需要 (1-p)k +(k+1)(1-(1-p)k)=(k+1)-k(1-p)k),在一個寫字中為
數學。
我們將 k 替換為 x 的實值數學,並尋找函式
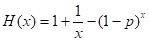
的最大點數學。
最小 H(x) 在 x0 處達到數學,其中 x0 是方程 H'(x) = 0 的較小根,即
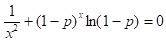
數學。
如果 p 很小(在真實情況下確實很小)數學,那麼透過將(1-p)x≈1-px, ln(1-p) ≈-p 來簡化,我們得到方程
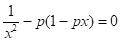
數學,其
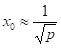
根是數學,則
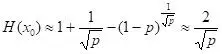
數學。
例如數學,如果 p=0.01,我們
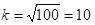
取,H(x) ≈ 0.2數學。這意味著檢測次數將減少 5 倍!
S.I. 多岑科 數學,基輔塔拉斯·舍甫琴科國立大學資訊科技學院物理與數學科學候選人副教授